Calculating the composite availability SLA for your stack

The following guide below will help you calculate your own availability.

Two parts to the guide according to what you are after.

• The actuarial science behind the calculation(which is just probability of "something" being available or unavailable)
• SLA Calculation guide to maximum downtime possible.

The Actuarial science

The calculation of service levels is purely to assess the risk or the probability of failure and taken as a mathematical problem.

Suggestion: Skip this if purely interested in just availability percentages. Go here

Let us consider the sample space of the following detail.

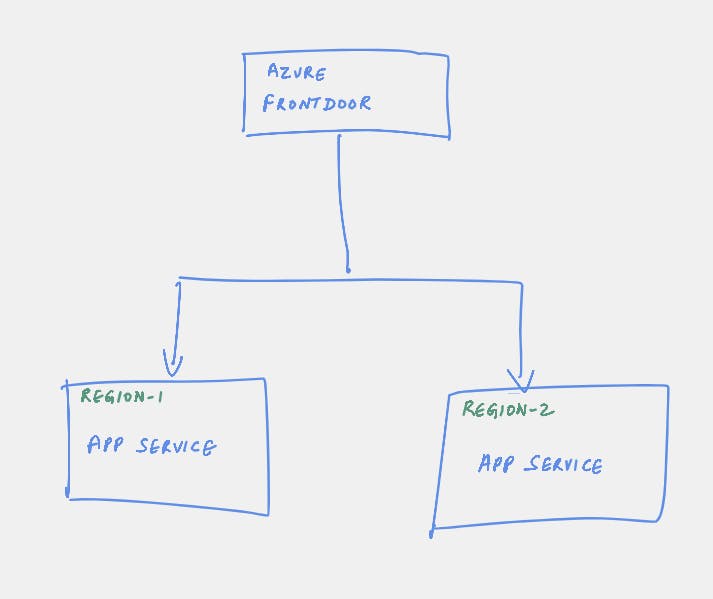
SLA summary for Azure services taken independently

• Azure DNS: 100% availability (so will remove from consideration in this problem, as will not skew the calculation)
• Azure Front door: 99.99% availability or 0.0001 probability of going down
• Azure App service: 99.95% availability or 0.0005 probability of going down

Note: Although App service is declared with an SLA of 99.95%, with the GA of zonal redundancy that should increase to 99.99% - but that has not been documented yet. For the case of this will be using as described here

Sample spaces for the probability:

Mutually exclusive events

• App service Region 1(AR1) is down but Azure Front door (FD is up)
• App service Region 2(AR2) is down but FD is up

Independent events

• AR1 and AR2 is down
• Azure Front door(FD) is down
• FD is down or AR1 and AR2 is down

For the Mutually exclusive events that either AR1 or AR2 is down, but not both simultaneously

P(AR1 and AR2) = P ( AR1 ∩ AR2 ) = 0

There by the probability of unavailability is 0 for the mutually exclusive events both occuring

For the Mutually exclusive events , then probability of either occuring

P(AR1 or AR2) = P(AR1 ∪ AR2 ) = (P(AR1) + P(AR2) - P(AR1 ∩ AR2) = P(AR1) + P(AR2) - 0 = P(AR1) + P(AR2)

calculating that as values

• Probability of AR1 to be down : 0.0005
• Probability of AR1 to be down : 0.0005

Probability of either to be down: P(AR1 and AR2) = 0.0005 + 0.0005 = 0.001

Calculating the probability of only operating on a single region

Two independent events

• Azure Front door being available = 1 - 0.0001 = 0.9999
• Either of AR1 or AR2 being available(AR1|AR2): 1 - 0.001 = 0.999

Overall probability of only being operational on a single region

P(FD and AR1|AR2) = P(FD ∪ AR1|AR2 )= P(FD)P(AR1|AR2) = 0.999 * 0.9999 = 0.9989001

In percentage = 99.89001%.

Overall availability/unavailability

Overall unavailability is the scenario FD is down or (AR1 and AR2) is down

• AR1 and AR2 are down as independent events AR1||AR2

  P(AR1 ∪ AR2) = P(AR1) * P(AR2) = 0.0005 * 0.0005 = 0.00000025

• FD is down as a independent event from AR1 and AR2 being down as independent events AR1||AR2

  P(FD ∩ AR1||AR2) = P(FD) * P(AR1||AR2) = 0.0001 * 0.00000025 = 0.00000000025

• FD is down as a mutually exclusive event from AR1 and AR2 being down as independent events, but either can occur

  P(FD U AR1||AR2) = P(FD) + P(AR1||AR2) - P(FD ∩ AR1||AR2)) = 0.0001 + 0.00000025 - 0.00000000025 = 0.00010025

Overall probability of availability = 1 - 0.00010025 = 0.99989975

In percentage: availability = 99.989975%

Calculating your downtime or availability percentages

The simplified calculation below just uses probability rules described above to calculate the compound availability of the stack.

Note: A few examples are given below to demon

Stack for a stateless web application

SLA calculation guide for the following detail:

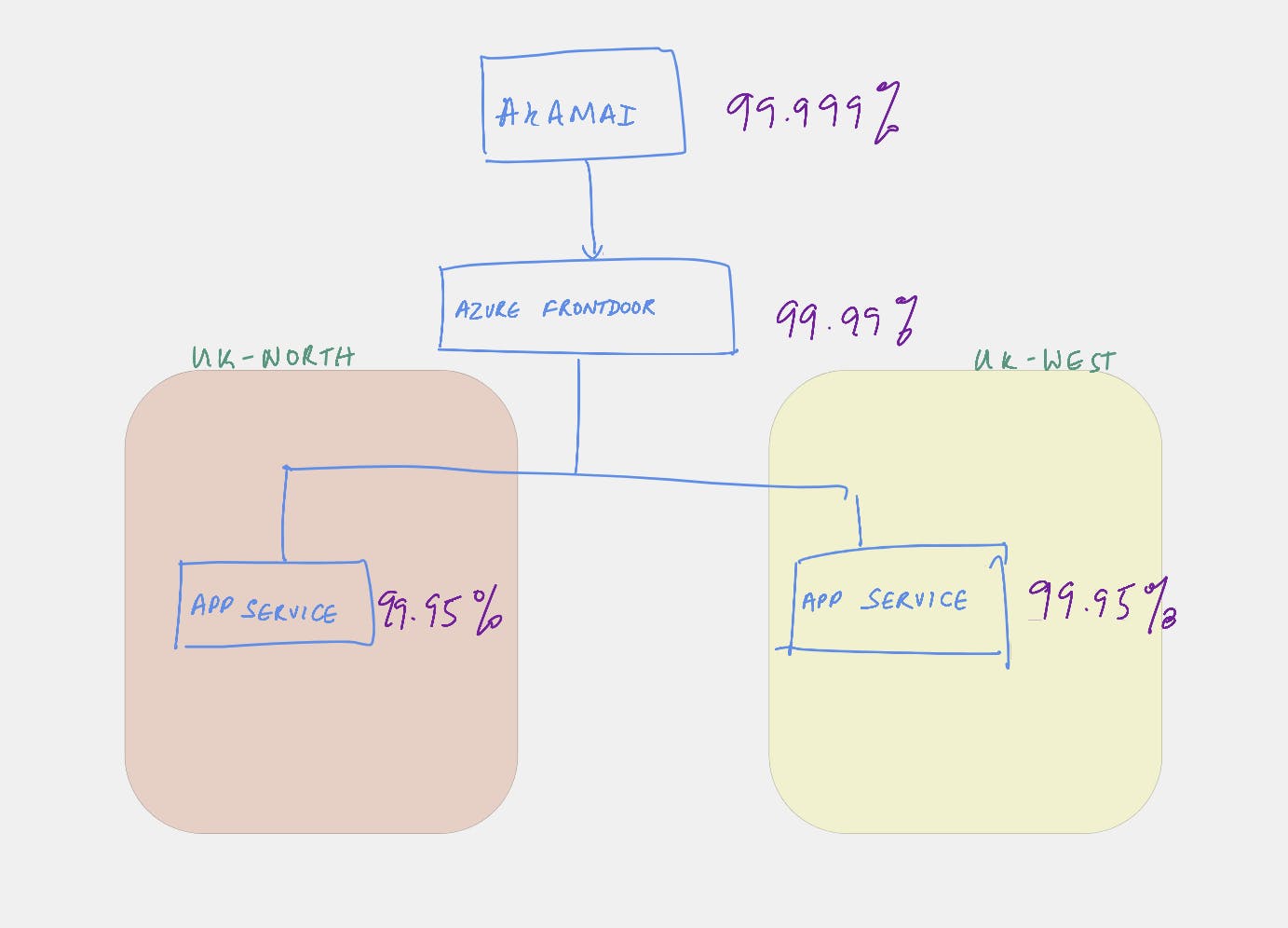
SLA summary for Azure services taken independently

• Akamai : 99.999%
• Azure DNS: 100% availability (so will remove from consideration in this problem, as will not skew the calculation)
• Azure Front door : 99.99% availability or 0.0001 probability of going down
• Azure App service: 99.95% availability or 0.0005 probability of going down

Azure App service across both regions being down as independent events simultaneously

0.05 % * 0.05 % = 0.000025%

So availability: 99.999975%

Either of Akamai OR Azure Frontdoor Or Azure App service across both regions being down

99.999% * 99.99% * 99.999975% = 99.9889%

The overall SLA of the stack is 99.9889%

Stack for a stateless web application through a private link with regional Redis cache

SLA calculation guide for the following detail:

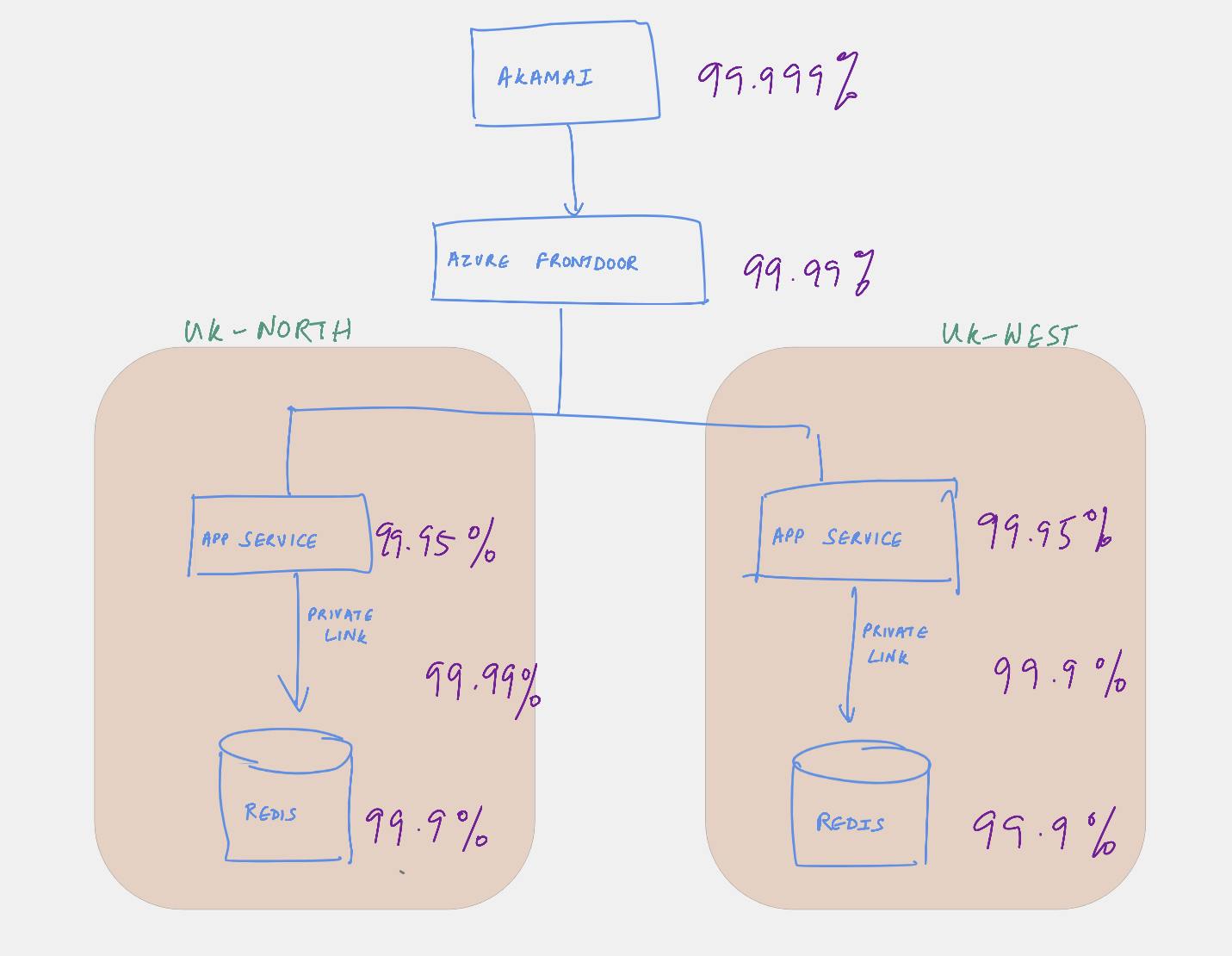
SLA summary for Azure services taken independently

• Akamai : 99.999%.(This could well be 100% - something to validate contractually)
• Azure DNS: 100% availability (so will remove from consideration in this problem, as will not skew the calculation)
• Azure Front door : 99.99% availability or 0.0001 probability of going down
• Azure App service: 99.95% availability or 0.0005 probability of going down
• Azure private link: 99.99% availability or 0.0001 probability of going down
• Azure Redis (individual region - for any Standard): 99.9% or 0.001 probability of going down

Although considering Redis being used as a cache (read/write through) and should not "really" affect the SLA, we would consider it technically as part of this calculation demonstration.

Composite Availability of App Service and Redis within a region (inclusive of private link)

99.95 % * 99.99% * 99.9 % = 99.84%

unavailability of a region : 0.16% (100 - 99.84)

Unavailability of two regions of App Service, private link and Redis.

0.16 % * 0.16 % = 0.000256%

Compound Availability of App service and Redis over two regions: 99.999744%

Compound availability of the stack (Akamai Frontdoor ( (appservice + redis)both regions) ))

99.999 % * 99.99% * 99.999744 % = 99.9887%

The overall SLA of the stack is 99.9887%

Follow the approach as in the above examples to calculate the composite availability of the stack you deploy appropriate to the configuration (eg: types of instances will have different SLAs premium vs standard)

Downtime calculation.

• For a 24 hour period, the maximum allowed downtime(error budget) for an availability of 99.9887% is 9.76 seconds $((100-99.9887)/100 24 3600))$
• For a month, the maximum allowed downtime is ~ 5 minutes